The Montessori method - ~幾何図形にまつわる活動から見るモンテッソーリ教育~
今回はモンテッソーリ活動の中に出てくる幾何図形からモンテッソーリ教育を見つめてみます。
モンテッソーリ環境
(子どもの発達に役に立つ道具=教具があり、その教具に子どもがどのように関わるといいのかを見せてくれる大人がいる環境)
には様々なところに”幾何図形の存在”があります。

こちらは感覚教育のエリアにある「構成三角形 長方形の箱2」という教具です。
同じ三角形を見つけ、それらを一組にして辺と辺を合わせると、ここでは長方形ができます。
その次にそれぞれの三角形をスライドさせ、別の辺と辺が合わさるようにすると今度は平行四辺形になります。
この教具は、三角形で色々な形を構成しながら、三角形の持つ構成力を知る体験を与えてくれます。
三角形の構成力とは、
全ての直線図形は、三角形に分けることができ、また逆に、全ての直線図形が三角形によって構成することができるということです。
もちろん幼児期の子どもたちにこのような抽象的な概念を言語で表現して伝えるわけにはいきません。
しかし幼児期(3−6歳)の子どもたちは、実際に手で触って、自分で動かして操作することができれば、言語化せずに、イメージとしてこうした抽象的な概念を感じとることができます。
そしてこのような体験が次の学童期(6−12歳)での学びを助けてくれるのです。
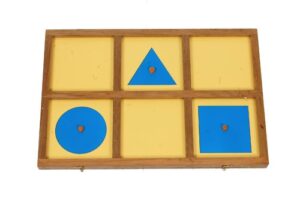
モンテッソーリ教育での幾何図形の最初の紹介は、この”幾何たんす”という教具で行います。
一番最初は「円、正三角形、正方形」です。
モンテッソーリ教育では初めから科学的な正式名称で紹介します。
子どもたちは、言語の敏感期であり、大人にとっては難しいイメージの言葉もすんなりと自分のものにしてしまう能力を持っているので、
こうした機会に、正式名称を取り込んでおくことで、後々親しみや自信を持って、学童期の学びにも臨めるようになるのです。
さて、この教具ですが、
一色だけの何の変哲もない「まる・さんかく・しかく」です。
何が面白いのでしょう。
まずは大人が幾何の魅力を知って、ワクワクした気持ちで子どもに紹介しなければなりません。
実は幾何の世界は魅力いっぱいです。
子どもたちがこのことに気づくことは、単に勉強ができる子になるだけではなく、
学び自体を楽しんで、その学び自体が豊かな人生そのものになるということにつながっていきます。
「円」は小さい子ども、とりわけ赤ちゃんにとってはとてもワクワクする形です。
それは生まれて初めて見る、お母さんの瞳の形だからです。
この瞳を見つめることは、赤ちゃんにとってとても大切なのです。
本当に人間の心理には円を特別に認識するものが組み込まれているのです。
モンテッソーリ博士は、Psychogeometryという幾何図形と人間の心理との関係性についての本を書いています。
日本語版はありませんが、興味深いですね。

「三角形」は最も少ない量の直線によって構成できる図形です。
次が「四角形」次が「五角形」「六角形」「七角形」・・・
幾何タンスの教具では「十角形」まで用意されています。
でももしもこのタンスが延々と続き、二十角形、三十角形、百角形、千角形・・・
さらに無限に続いたら最後にはどんな図形になるでしょうか。


なんとそれは「円」なのです。
多角形のカクカクした部分が増えれば増えるほど丸みをおび、最終的にはツルツルになるでしょう。
それが円なのです。
つまりこうしてみると「三角形」が始まりで、「四角形」は途中で「円」が最終形態なのです。
驚きの発見だし、なんだかワクワクを感じませんか?
これがセンス・オブ・ワンダーであり、学びを豊かな味わい深いものにするものなのです。
今度は三角形だけに注目してみましょう。
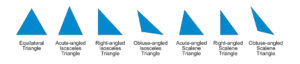
幾何タンスには、正三角 直角二等辺三角形 直角不等辺三角形 鈍角二等辺三角形 鈍角不等辺三角形 鋭角二等辺三角形、鋭角不等辺三角形の7つの三角形が入っています。
この漢字で示された名前は実に難しそうですが、子どもたちは漢字なしに、音と形のイメージで自分のものにしてしまいます。
どうしてこの7種類の三角形というと、なんとこの7種類以外の三角形は世界のどこにも存在しないからなんです。
実際にこの7種類の三角形を覚えてしまったお子さんは、ある時、部屋の床に日の光が差し込み、そこに椅子や机の影ができ、たまたま三角形ができているのを見ました。
そしてそれが自分が知っている7種類の三角形のどれなのかを特定しようと、まじまじと観察し、
見事言い当てることができ、大きな声で感動を味わっていました。
また、ある時はハサミ切りのお仕事で紙を切った時の紙屑が三角形になっていていることを発見し、
その時もまた同じお子さんが、「これは、鈍角二等辺三角形だ~」と感極まっていました。

この7つの三角形は、子どもを言語の世界にも導いてくれます。
それが、形容詞の探偵ゲームです。
この7つの三角形に親しんだお子さんが行うことができます。
青・赤・黄の3色のものがあり、サイズが大・中・小に別れ、それぞれに7つの三角形があります。
つまり7X3X3=63枚の三角形があります。
このゲームでは、探偵になって、先生が出すヒントに従って1枚の三角形を見つけ出します。
例えば「あおい おおきい えいかく ふとうへん さんかくけい」です。
この活動は、名詞を修飾する言葉、形容詞などの言葉
(子ども向きには「どんなものか教えてくれる言葉」)
が持つ「特定する力」に気づくことが目的です。
よくニュースで聞くような、
「20代男性、身長170cm、短髪、黒のジャージを着用」などがそれです。
名詞を修飾する言葉が重なれば重なるほど、特定しやすくなります。
このようにモンテッソーリ教育では幾何図形を用いて、感覚教育、幾何学、言語教育にわたって子どもに様々な探索や発見の機会を与えることができるのです。
様々な教科が同じ部屋で同じ時間に行われるの理由のひとつは、
それぞれの知識がお互いに関連していて、合わさることで、より完全な理解になっていくからです。
これがモンテッソーリ教育がホリスティック(統合的な)教育と呼ばれる理由のひとつです。
ひとつひとつの学びが、後になって点と点が結ばれ線になり、
線と線が合わさり面になり、面と面が合わさり立体になるように、
理解が合わさり、完成されていくのです。
数教育、言語教育、感覚教育、日常生活の練習は、別々の世界ではなく、
数教育、言語教育、感覚教育、日常生活の練習というレンズを通して、ひとつの世界を理解しようとしているということなのです。
モンテッソーリ教育の意義の一つは、
この一つの世界(現実の世界)を探索するための鍵を子どもたちに与えることなのです。
さて、
今回はモンテッソーリの幾何図形にまつわる活動をもとに、
モンテッソーリ教育が教科ごとの枠を超えて、感覚や言語など様々な観点から、
一見難しそうな抽象的なことを視覚や五感を使って感覚的に取り込み、
実際に手で操作しながら学び、
またそれをいかに実生活に応用して自分のものにしていくかについて、ご紹介させていただきました。

